PID Control (3)

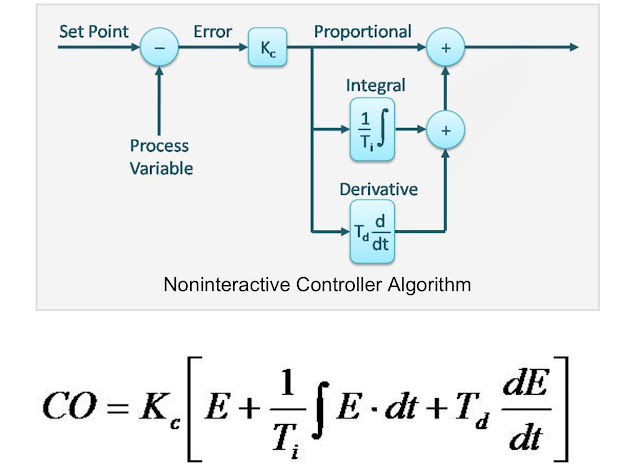
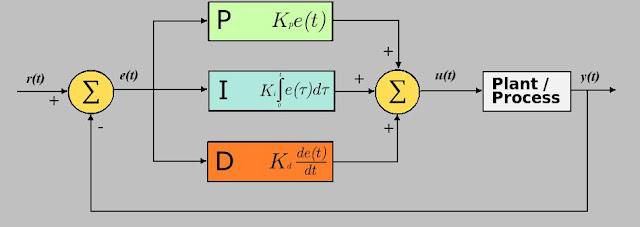
ဒီတစ္ခါ Tuning အပိုင္း ေျပာျပပါမယ္။ စာအုပ္ထဲက formula ေတြ ပါလာတာမို႔ စိတ္ရွည္ရွည္နဲ႔ ႀကိဳးစား ဖတ္ၾကည့္ၾကပါ။
Tuning လုပ္မယ္ဆိုရင္ လိုခ်င္တဲ့ရလဒ္က ႏွစ္မ်ဳိးရွိပါတယ္။ အဲဒါကေတာ့ တုန္႔ျပန္မႈ ျမန္ျမန္ (fast response) နဲ႔ တည္ၿငိမ္မႈ ေကာင္းေကာင္း (good stability) ပါ။ တစ္ကယ့္လက္ေတြ႕မွာေတာ့ အဲဒီႏွစ္ခုလုံး အေကာင္းဆုံး ၿပိဳင္တူရဖို႔ မလြယ္ပါဘူး။ ဒီေတာ့ လက္ခံႏိုင္ေလာက္တဲ့ တည္ၿငိမ္မႈရယ္၊ ထိုက္သင့္တဲ့ အခ်ိန္တိုအတြင္းရတဲ့ တုန္႔ျပန္မႈရယ္ ရေအာင္ ခ်ိန္ႏိုင္ရင္ ေတာ္ပါၿပီ။

Tune မလုပ္ခင္ Parameter ေတြရဲ႕ သက္ေရာက္ပုံေလး သိထားသင့္ပါတယ္။ Steady state တစ္ခုကေန Step အေျပာင္းအလဲလုပ္လိုက္ရင္ ျဖစ္လာတဲ့ သက္ေရာက္မႈ (reactive curve) ကိုၾကည့္ၿပီး သတိထားရမယ့္ အခ်က္ေတြက ဒီ ၄ ခုကို ၾကည့္ပါတယ္။
(i) Rise Time (ပထမဆုံး အႀကိမ္ PV Level အသစ္ကို ေရာက္ဖို႔ ၾကာခ်ိန္)
(ii) Overshoot (ေနာက္ Level ကို လြန္သြားတဲ့ peak ပမာဏ)
(iii) Settling Time (Steady State ျပန္ရဖို႔ ၾကာခ်ိန္)
(iv) Steady State Error ( Steady State ေရာက္ေပမဲ့ SP နဲ႔ ကြာေနတဲ့ တန္ဖိုး - Offset)

P, I, D တစ္ခုစီက ဒီ အခ်က္ ၄ ခုကို ဘယ္လို သက္ေရာက္ေစတယ္ဆိုတာ ဇယားမွာ ၾကည့္ပါ။

Tuning parameter ေတြကို အရင္ ျပန္ၾကည့္ရေအာင္။ Parameter ေတြက controller ထုတ္လုပ္တဲ့သူ ေပၚမူတည္ၿပီး အမ်ဳိးမ်ဳိးကြဲႏိုင္ပါတယ္။
- Proportional အတြက္ parameter က Gain (Kp) ဒါမွမဟုတ္ Proportional Band (PB) ျဖစ္ပါတယ္။
- Integral အတြက္ parameter က Reset rate (Ki) ဒါမွမဟုတ္ reset time (Ti) ပါ။ ကိုယ္သုံးတဲ့ controller / program ေပၚ မူတည္ပါတယ္။
- Derivative အတြက္ parameter ကေတာ့ Kd ဒါမွမဟုတ္ Td ပါ။

Tune လုပ္တဲ့ နည္းအမ်ဳိးမ်ဳိးရွိပါတယ္။ အဲဒီထဲက လူသိမ်ားတဲ့ နည္းေတြ ျဖစ္တဲ့ ေအာက္က နည္း ၃ မ်ဳိး နဲ႔ Manual Tuning ေတြကိုေျပာျပပါမယ္။

a) Ziegler Nichols Open Loop  Method
b) Ziegler Nichols Closed Loop  Method
c) Cohen Coon Tuning Method
d) Manual Tuning Method

အဲဒီနည္းေတြရဲ႕ ေကာင္းကြက္ ဆိုးကြက္ေတြရွိသလို၊ တစ္ခ်ဳိ႕နည္းေတြမွာ သံုးႏိုင္တဲ့ Controller အမ်ဳိးအစား ကန္သတ္ခ်က္ေတြရွိပါတယ္။

a) Ziegler Nichols Open Loop Method

ဒီနည္းကို Process Reaction Curve Method လို႔လည္း ေခၚၾကပါတယ္။ Tuning အဆင့္ေတြကို ေအာက္မွာ ေရးျပထားပါတယ္။
1. ပထမဆုံး PV Output Level တစ္ခုရေအာင္ manual mode မွာ ညႇိေပးပါ။
2. Step input တစ္ခုေပးလိုက္ပါ။
3. ေျပာင္းသြားတဲ့ PV တန္ဖိုးေတြကို Level အသစ္မွာ တည္ၿငိမ္မႈ ရတဲ့အထိ ေစာင့္ၿပီး plot လုပ္ပါ။ အဲဒါကို Process Reaction Curve (သို႔) S ပုံစံရွိလို႔ S-curve လို႔ ေခၚပါတယ္။
4. အဲဒီ curve ေပၚမွာ point တစ္ခုစီရဲ႕ tangent line ဆြဲရင္ slope အမ်ားဆုံးရတဲ့ tangent line ကိုဆြဲပါ။
5. အဲဒီ tangent line က မူလ PV Level ကို ျဖတ္သြားတဲ့ အမွတ္ရယ္၊ Level အသစ္ရယ္ကို ျဖတ္သြားတဲ့ အမွတ္ရယ္ ရပါမယ္။
6. အဲဒီအမွတ္ေတြေပၚမူတည္ၿပီး L နဲ႔ T ရဲ႕တန္ဖိုးေတြ ရပါလိမ့္မယ္။ (ပုံကို ၾကည့္ပါ။) L ကို Dead time (သို႔) Delay time လို႔ ေခၚပါတယ္။ T ကေတာ့ Time Constant လို႔ ေခၚပါတယ္။
7. အဲဒီ L နဲ႔ T တန္ဖိုးေတြ သုံးၿပီး ဇယားမွာပါတဲ့ အတိုင္း တြက္လိုက္ရင္ Kp, Ti, Td တန္ဖိုးေတြ ရပါလိမ့္မယ္။ ( ဇယား ကိုၾကည့္ပါ။)

b)  Ziegler Nichols Closed Loop Method

ဒီနည္းကို Ultimate Gain Method လို႔လည္း ေခၚပါတယ္။
1. အစဆုံး Manual mode နဲ႔ SP နဲ႔ PV ကိုတူတဲ့အထိ ညိႇလိုက္ပါ။
2. P တစ္မ်ဳိးပဲ သုံးၿပီး Control လုပ္ပါ။ ဆိုလိုတာက P တန္ဖိုး နိမ့္နိမ့္ တစ္ခုထားၿပီး I နဲ႔ D တန္ဖိုးေတြ 0 ထားၿပီး disable လုပ္ရမွာပါ။ (Ti ဆိုရင္ေတာ့ infinity ထားရပါမယ္။ Disable ဘယ္လိုလုပ္ရမယ္ဆိုတာ Maker ရဲ႕ လမ္းၫႊန္ ဖတ္ၾကည့္ပါ။)
3. SP ကို 5% ေလာက္ေျပာင္းၿပီး step input ေပးလိုက္ပါ။
4. PV တန္ဖိုးကိုၾကည့္ၿပီး P တန္ဖိုးကို အတင္၊ အခ် Tune လုပ္ပါ။ တစ္ခ်ိန္မွာ Steady Oscillation လို႔ေခၚတဲ့ တည္ၿငိမ္ၿပီး တန္ဖိုးညီညာတဲ့ လိႈင္းပုံျဖစ္လာတဲ့အထိ ညိႇပါ။ (ပုံမွာ ၾကည့္ပါ။)
5. အဲဒီလိုရတဲ့ gain (သို႔) Kp တန္ဖိုးကို Ultimate Gain (သို႔) Critical Gain (Kcr) လို႔ ေခၚပါတယ္။
6. လႈိင္းထိပ္ ႏွစ္ခုအကြာအေဝး၊ ၾကာခ်ိန္ကို Pcr လို႔ ထားပါ။
7. အဲဒီ Kcr နဲ႔ Pcr ေပၚမူတည္ၿပီး သူတို႔ recommend လုပ္တဲ့ Kp, Ti, Td တန္ဖိုးေတြကို ေအာက္က ဇယားမွာ ၾကည့္ုၿပီး တြက္ထုတ္လို႔ ရပါၿပီ။ လိုအပ္ရင္ fine tune လုပ္ေပးရပါတယ္။

c) Cohen Coon Tuning Method

ဒီနည္းကေတာ့ Z-C Open Loop နည္းနဲ႔ ဆင္တူပါတယ္။ ဒါေပမဲ့ တြက္တဲ့နည္းေတြက ပိုရႈပ္ပါတယ္။
အဆင့္ (1-4) က Z-C Open Loop အတိုင္း အတူတူပါဘဲ။
5. PV Level ႏွစ္ခု ျခားနားခ်က္ ရဲ႕ 63.2% ကို curve ျဖတ္သြားတဲ့ အမွတ္ နဲ႔ 28.3% ကို ျဖတ္သြားတဲ့ အမွတ္ ေတြေပၚမူတည္ၿပီး Delay time (td) နဲ႔ time constant (Tm) ေတြ တြက္ထုတ္ပါတယ္။ (ပုံမွာ ၾကည့္ပါ။)
6. Process Gain (Km) = Change in PV (%) / Change in CO (%) နည္းနဲ႔ Km ကို တြက္ယူပါတယ္။
7. အဲဒီ td, Tm, Km သုံးၿပီး Kp, Ti, Td တန္ဖိုးေတြကို ဇယားထဲက အတိုင္း တြက္ထုတ္ႏိုင္ပါတယ္။ (ဇယား ၾကည့္ပါ။)

d) Manual Tuning

အေပၚက နည္းေတြသုံးဖို႔ ျပႆနာ တစ္ခုရွိပါတယ္။ အဲဒါကေတာ့ Output တန္ဖိုး (PV) ကို curve ဆြဲၿပီး တြက္ထုတ္ဖို႔ လိုပါတယ္။ တစ္ခ်ဳိ႕ PC based controller ေတြမွာ ဒီလို curve ေတြ plot လုပ္လို႔ ရေပမဲ့ ေတာ္ေတာ္မ်ားမ်ား controller ေတြမွာ plot လုပ္ဖို႔ မလြယ္ပါဘူး။ ဒါေၾကာင့္ ေနာက္ဆုံးနည္း ျဖစ္တဲ့ Manual Tuning ကို ထည့္ေျပာျပမွာပါ။

(1-4) အဆင့္ ေတြကေတာ့ Z-C Closed Loop နည္းအတိုင္း လုပ္ပါ။ Oscillation ျဖစ္တာကို Curve မဆြဲပဲ တန္ဖိုး ေျပာင္းတာ သတိထားၾကည့္ရင္ သိႏိုင္ပါတယ္။
5. D ကို တင္ေပးၿပီး Oscillation ေပ်ာက္ေအာင္ညႇိပါ။
6. I တန္ဖိုးကိုတင္ၿပီး offset မရွိေအာင္ညိႇပါ။
7. တည္ၿငိမ္မႈ မရွိရင္ P နဲ႔ D ကို နည္းနည္းစီ ျပန္ ညိႇေပးပါ။

ေနာက္ဆုံး ျပန္ျခဳံေျပာရရင္၊
- Rise time ျမန္ေအာင္ ညႇိခ်င္ရင္ P ကိုသုံးပါ။
- Overshoot နဲ႔ Settling time နည္းေအာင္ ညွိခ်င္ရင္ D ကိုသုံးပါ။
- Offset ေပ်ာက္ေအာင္ ညိႇခ်င္ရင္ I ကိုသုံးပါ။

Auto Tuning

ေနာက္ထြက္တဲ့ PID Controller ေတြမွာ Auto Tuning function ပါေလ့ရွိပါတယ္။ ဒါဆိုရင္ေတာ့ အရမ္းလြယ္သြားပါၿပီ။ Auto Tune function ကို run လိုက္တာနဲ႔ Controller က Simulated Set Point နဲ႔ disturbance ေတြ ေပးပါတယ္။ ထြက္လာတဲ့ Response အရ Controller က learn လုပ္ၿပီး PID parameter ေတြ အလိုအေလ်ာက္ tune လုပ္ေပးမွာပါ။

ေက်းဇူးတင္ပါတယ္။

[Unicode]


ဒီတစ်ခါ Tuning အပိုင်း ပြောပြပါမယ်။ စာအုပ်ထဲက formula တွေ ပါလာတာမို့ စိတ်ရှည်ရှည်နဲ့ ကြိုးစား ဖတ်ကြည့်ကြပါ။
Tuning လုပ်မယ်ဆိုရင် လိုချင်တဲ့ရလဒ်က နှစ်မျိုးရှိပါတယ်။ အဲဒါကတော့ တုန့်ပြန်မှု မြန်မြန် (fast response) နဲ့ တည်ငြိမ်မှု ကောင်းကောင်း (good stability) ပါ။ တစ်ကယ့်လက်တွေ့မှာတော့ အဲဒီနှစ်ခုလုံး အကောင်းဆုံး ပြိုင်တူရဖို့ မလွယ်ပါဘူး။ ဒီတော့ လက်ခံနိုင်လောက်တဲ့ တည်ငြိမ်မှုရယ်၊ ထိုက်သင့်တဲ့ အချိန်တိုအတွင်းရတဲ့ တုန့်ပြန်မှုရယ် ရအောင် ချိန်နိုင်ရင် တော်ပါပြီ။

Tune မလုပ်ခင် Parameter တွေရဲ့ သက်ရောက်ပုံလေး သိထားသင့်ပါတယ်။ Steady state တစ်ခုကနေ Step အပြောင်းအလဲလုပ်လိုက်ရင် ဖြစ်လာတဲ့ သက်ရောက်မှု (reactive curve) ကိုကြည့်ပြီး သတိထားရမယ့် အချက်တွေက ဒီ ၄ ခုကို ကြည့်ပါတယ်။
(i) Rise Time (ပထမဆုံး အကြိမ် PV Level အသစ်ကို ရောက်ဖို့ ကြာချိန်)
(ii) Overshoot (နောက် Level ကို လွန်သွားတဲ့ peak ပမာဏ)
(iii) Settling Time (Steady State ပြန်ရဖို့ ကြာချိန်)
(iv) Steady State Error ( Steady State ရောက်ပေမဲ့ SP နဲ့ ကွာနေတဲ့ တန်ဖိုး - Offset)

P, I, D တစ်ခုစီက ဒီ အချက် ၄ ခုကို ဘယ်လို သက်ရောက်စေတယ်ဆိုတာ ဇယားမှာ ကြည့်ပါ။

Tuning parameter တွေကို အရင် ပြန်ကြည့်ရအောင်။ Parameter တွေက controller ထုတ်လုပ်တဲ့သူ ပေါ်မူတည်ပြီး အမျိုးမျိုးကွဲနိုင်ပါတယ်။
- Proportional အတွက် parameter က Gain (Kp) ဒါမှမဟုတ် Proportional Band (PB) ဖြစ်ပါတယ်။
- Integral အတွက် parameter က Reset rate (Ki) ဒါမှမဟုတ် reset time (Ti) ပါ။ ကိုယ်သုံးတဲ့ controller / program ပေါ် မူတည်ပါတယ်။
- Derivative အတွက် parameter ကတော့ Kd ဒါမှမဟုတ် Td ပါ။

Tune လုပ်တဲ့ နည်းအမျိုးမျိုးရှိပါတယ်။ အဲဒီထဲက လူသိများတဲ့ နည်းတွေ ဖြစ်တဲ့ အောက်က နည်း ၃ မျိုး နဲ့ Manual Tuning တွေကိုပြောပြပါမယ်။

a) Ziegler Nichols Open Loop  Method
b) Ziegler Nichols Closed Loop  Method
c) Cohen Coon Tuning Method
d) Manual Tuning Method

အဲဒီနည်းတွေရဲ့ ကောင်းကွက် ဆိုးကွက်တွေရှိသလို၊ တစ်ချို့နည်းတွေမှာ သုံးနိုင်တဲ့ Controller အမျိုးအစား ကန်သတ်ချက်တွေရှိပါတယ်။

a) Ziegler Nichols Open Loop Method

ဒီနည်းကို Process Reaction Curve Method လို့လည်း ခေါ်ကြပါတယ်။ Tuning အဆင့်တွေကို အောက်မှာ ရေးပြထားပါတယ်။
1. ပထမဆုံး PV Output Level တစ်ခုရအောင် manual mode မှာ ညှိပေးပါ။
2. Step input တစ်ခုပေးလိုက်ပါ။
3. ပြောင်းသွားတဲ့ PV တန်ဖိုးတွေကို Level အသစ်မှာ တည်ငြိမ်မှု ရတဲ့အထိ စောင့်ပြီး plot လုပ်ပါ။ အဲဒါကို Process Reaction Curve (သို့) S ပုံစံရှိလို့ S-curve လို့ ခေါ်ပါတယ်။
4. အဲဒီ curve ပေါ်မှာ point တစ်ခုစီရဲ့ tangent line ဆွဲရင် slope အများဆုံးရတဲ့ tangent line ကိုဆွဲပါ။
5. အဲဒီ tangent line က မူလ PV Level ကို ဖြတ်သွားတဲ့ အမှတ်ရယ်၊ Level အသစ်ရယ်ကို ဖြတ်သွားတဲ့ အမှတ်ရယ် ရပါမယ်။
6. အဲဒီအမှတ်တွေပေါ်မူတည်ပြီး L နဲ့ T ရဲ့တန်ဖိုးတွေ ရပါလိမ့်မယ်။ (ပုံကို ကြည့်ပါ။) L ကို Dead time (သို့) Delay time လို့ ခေါ်ပါတယ်။ T ကတော့ Time Constant လို့ ခေါ်ပါတယ်။
7. အဲဒီ L နဲ့ T တန်ဖိုးတွေ သုံးပြီး ဇယားမှာပါတဲ့ အတိုင်း တွက်လိုက်ရင် Kp, Ti, Td တန်ဖိုးတွေ ရပါလိမ့်မယ်။ ( ဇယား ကိုကြည့်ပါ။)

b)  Ziegler Nichols Closed Loop Method
ဒီနည်းကို Ultimate Gain Method လို့လည်း ခေါ်ပါတယ်။
1. အစဆုံး Manual mode နဲ့ SP နဲ့ PV ကိုတူတဲ့အထိ ညှိလိုက်ပါ။
2. P တစ်မျိုးပဲ သုံးပြီး Control လုပ်ပါ။ ဆိုလိုတာက P တန်ဖိုး နိမ့်နိမ့် တစ်ခုထားပြီး I နဲ့ D တန်ဖိုးတွေ 0 ထားပြီး disable လုပ်ရမှာပါ။ (Ti ဆိုရင်တော့ infinity ထားရပါမယ်။ Disable ဘယ်လိုလုပ်ရမယ်ဆိုတာ Maker ရဲ့ လမ်းညွှန် ဖတ်ကြည့်ပါ။)
3. SP ကို 5% လောက်ပြောင်းပြီး step input ပေးလိုက်ပါ။
4. PV တန်ဖိုးကိုကြည့်ပြီး P တန်ဖိုးကို အတင်၊ အချ Tune လုပ်ပါ။ တစ်ချိန်မှာ Steady Oscillation လို့ခေါ်တဲ့ တည်ငြိမ်ပြီး တန်ဖိုးညီညာတဲ့ လှိုင်းပုံဖြစ်လာတဲ့အထိ ညှိပါ။ (ပုံမှာ ကြည့်ပါ။)
5. အဲဒီလိုရတဲ့ gain (သို့) Kp တန်ဖိုးကို Ultimate Gain (သို့) Critical Gain (Kcr) လို့ ခေါ်ပါတယ်။
6. လှိုင်းထိပ် နှစ်ခုအကွာအဝေး၊ ကြာချိန်ကို Pcr လို့ ထားပါ။
7. အဲဒီ Kcr နဲ့ Pcr ပေါ်မူတည်ပြီး သူတို့ recommend လုပ်တဲ့ Kp, Ti, Td တန်ဖိုးတွေကို အောက်က ဇယားမှာ ကြည့်ုပြီး တွက်ထုတ်လို့ ရပါပြီ။ လိုအပ်ရင် fine tune လုပ်ပေးရပါတယ်။

c) Cohen Coon Tuning Method
ဒီနည်းကတော့ Z-C Open Loop နည်းနဲ့ ဆင်တူပါတယ်။ ဒါပေမဲ့ တွက်တဲ့နည်းတွေက ပိုရှုပ်ပါတယ်။
အဆင့် (1-4) က Z-C Open Loop အတိုင်း အတူတူပါဘဲ။
5. PV Level နှစ်ခု ခြားနားချက် ရဲ့ 63.2% ကို curve ဖြတ်သွားတဲ့ အမှတ် နဲ့ 28.3% ကို ဖြတ်သွားတဲ့ အမှတ် တွေပေါ်မူတည်ပြီး Delay time (td) နဲ့ time constant (Tm) တွေ တွက်ထုတ်ပါတယ်။ (ပုံမှာ ကြည့်ပါ။)
6. Process Gain (Km) = Change in PV (%) / Change in CO (%) နည်းနဲ့ Km ကို တွက်ယူပါတယ်။
7. အဲဒီ td, Tm, Km သုံးပြီး Kp, Ti, Td တန်ဖိုးတွေကို ဇယားထဲက အတိုင်း တွက်ထုတ်နိုင်ပါတယ်။ (ဇယား ကြည့်ပါ။)

d) Manual Tuning
အပေါ်က နည်းတွေသုံးဖို့ ပြဿနာ တစ်ခုရှိပါတယ်။ အဲဒါကတော့ Output တန်ဖိုး (PV) ကို curve ဆွဲပြီး တွက်ထုတ်ဖို့ လိုပါတယ်။ တစ်ချို့ PC based controller တွေမှာ ဒီလို curve တွေ plot လုပ်လို့ ရပေမဲ့ တော်တော်များများ controller တွေမှာ plot လုပ်ဖို့ မလွယ်ပါဘူး။ ဒါကြောင့် နောက်ဆုံးနည်း ဖြစ်တဲ့ Manual Tuning ကို ထည့်ပြောပြမှာပါ။

(1-4) အဆင့် တွေကတော့ Z-C Closed Loop နည်းအတိုင်း လုပ်ပါ။ Oscillation ဖြစ်တာကို Curve မဆွဲပဲ တန်ဖိုး ပြောင်းတာ သတိထားကြည့်ရင် သိနိုင်ပါတယ်။
5. D ကို တင်ပေးပြီး Oscillation ပျောက်အောင်ညှိပါ။
6. I တန်ဖိုးကိုတင်ပြီး offset မရှိအောင်ညှိပါ။
7. တည်ငြိမ်မှု မရှိရင် P နဲ့ D ကို နည်းနည်းစီ ပြန် ညှိပေးပါ။

နောက်ဆုံး ပြန်ခြုံပြောရရင်၊
- Rise time မြန်အောင် ညှိချင်ရင် P ကိုသုံးပါ။
- Overshoot နဲ့ Settling time နည်းအောင် ညှိချင်ရင် D ကိုသုံးပါ။
- Offset ပျောက်အောင် ညှိချင်ရင် I ကိုသုံးပါ။

Auto Tuning
နောက်ထွက်တဲ့ PID Controller တွေမှာ Auto Tuning function ပါလေ့ရှိပါတယ်။ ဒါဆိုရင်တော့ အရမ်းလွယ်သွားပါပြီ။ Auto Tune function ကို run လိုက်တာနဲ့ Controller က Simulated Set Point နဲ့ disturbance တွေ ပေးပါတယ်။ ထွက်လာတဲ့ Response အရ Controller က learn လုပ်ပြီး PID parameter တွေ အလိုအလျောက် tune လုပ်ပေးမှာပါ။

ကျေးဇူးတင်ပါတယ်။

PID Control (2)

(က) P, PI, PID

ဒီတစ္ခါ ဥပမာေလး တစ္ခုနဲ႔ စေျပာပါမယ္။ ဘြိဳင္လာ (Boiler) တစ္လုံးရဲ႕ ေရ level ထိန္းခ်ဳပ္တဲ့ စံနစ္ေလးတစ္ခုကို ျမင္ၾကည့္ရေအာင္။ ေရရဲ႕ level ကို Set Point (SP) input အေနနဲ႔ ေပးထားၿပီး တည္ၿငိမ္ေအာင္ ထိန္းခ်ဳပ္မယ္ဆိုပါေတာ့။ ေရအထြက္နႈံးကေတာ့ Boiler မွာသုံးတဲ့ ေရေႏြးေငြ႕ အထြက္ေပၚမူတည္ေနပါတယ္။ အဲဒီအပိုင္းကို Control ရႈေထာင့္ကၾကည့္ယင္ loading ဒါမွမဟုတ္ disturbance လို႔ ေခၚပါတယ္။ Control လုပ္ေပးမယ့္ process ကေတာ့ ေရအဝင္နႈံး။ အေသးစိတ္ေျပာရယင္ေတာ့ water inlet valve ရဲ႕ အက်ဥ္းအက်ယ္ ဖြင့္တာပိတ္တာကို PID နဲ႔ Control လုပ္မယ္ ဆိုပါေတာ့။ Feedback (PV) ကေတာ့ ေရ level transmitter တစ္ခုပါ။ လိုခ်င္တဲ့ ေရ level (SP) ကို tank ရဲ႕ 50% မွာ ထားတယ္ ဆိုပါေတာ့။

အစဆုံး လက္ရွိအေျခအေနမွာ၊ Proportional (P) တစ္ခုဘဲ သုံးထားၿပီး၊ ေရ အဝင္အထြက္နႈံးေတြ တူေနတဲ့အတြက္၊ တစ္ကယ္တိုင္းလို႔ရတဲ့ Feedback (PV) ကလည္း 50% မွာ steady state ျဖစ္ေနတယ္လို႔ ယူဆပါ။

Controller Output(CO) (သို႔) Manipulated Variable (MV) (သို႔) u(t) ရဲ႕ ညီမွ်ျခင္းက

u(t) = Kp e(t) 

ဒီေနရာမွာ 

- Kp ဆိုတာ proportional gain

- e(t) ဆိုတာ Error (သို႔) SP - PV

တစ္ခါတေလ Kp အစား Proportional Band (PB) ကိုသုံးတာလည္း ရွိတတ္ပါတယ္။

PB = 100/Kp [%] 

အဲဒီအေနအထားကေန loading ပိုလာတဲ့အတြက္ ေရအထြက္နႈံး ပိုမ်ားလာတယ္ ဆိုပါေတာ့။ Tank ထဲက ေရ level ေလ်ာ့သြားေတာ့ SP-PV = Error တန္ဘိုးတစ္ခုရွိလာပါတယ္။ လက္ရွိ Kp (သို႔) Proportional gain တန္ဘိုးက 2% ဆိုယင္ Error နဲ႔ gain ေျမႇာက္ၿပီး valve အက်ဥ္းအက်ယ္ေျပာင္းေပးၿပီး Control လုပ္ေပးတာ ေနာက္ဆုံး ေရ အဝင္နႈံးနဲ႔ အထြက္နႈံး ညီသြားေတာ့ steady state ကိုေရာက္သြားပါတယ္။ အဲဒီ အခ်ိန္မွာ Tank ရဲ႕ level က 45% ေလာက္ထိ ေလ်ာ့ေနပါၿပီ။ SP နဲ႔ ယွဥ္လိုက္ေတာ့ 5% နည္းေနတာေပါ့။ အဲဒီလိုstable state ေရာက္ၿပီး offset ျဖစ္ေနတတ္တာက P တစ္ခုထဲ Control လုပ္ယင္ ျဖစ္တတ္တဲ့ အားနည္းခ်က္ပါ။ 

တစ္ကယ္လို႔ gain မ်ားမယ္ဆိုယင္ ေစာေစာစီးစီး steady state ေရာက္သြားတဲ့အတြက္ offset တန္ဘိုး နည္းမွာပါ။ Gain တန္ဘိုး infinity ေလာက္ထိ တင္ေပးထားယင္ေတာ့ offset မရွိေတာ့ဘူးလို႔ ဆိုပါတယ္။ ဒါေပမဲ့ လက္ေတြ႕မွာ gain ကို infinity ထိတင္ေပးတယ္ဆိုတာ မျဖစ္ႏိုင္ပါဘူး။ ဒီေတာ့ offset ျဖစ္ေနတဲ့ ေရ level ကို ျပန္ျဖည့္ေပးဘို႔ လိုပါတယ္။

ပထမနည္းကေတာ့ Manually inlet valve ကို ပိုဖြင့္ေပးတဲ့ နည္းပါ။ အဲဒါကို reset လုပ္တယ္လို႔ ေခၚပါတယ္။ ေနာက္တစ္နည္းကေတာ့ Integral Control (I) ကို သုံးတဲ့နည္းပါဘဲ။ အခ်ိန္တစ္ခုေရာက္တိုင္း အလိုအေလ်ာက္ reset လုပ္ေပးတဲ့ သေဘာပါ။ I ရဲ႕ Control parameter ျဖစ္တဲ့ Ki ဆိုတာ reset rate ေပါ့။ Controller ထုတ္လုပ္တဲ့ manufacturer ေပၚမူတည္ၿပီး I ရဲ႕Control parameter ႏွစ္မ်ဳိး ေတြ႕ႏိုင္ပါတယ္။ တစ္မိနစ္ အတြင္း reset လုပ္တဲ့ အႀကိမ္ေရ (repeat per minute) Ki နဲ႔ reset လုပ္ရမယ့္ ၾကာခ်ိန္ (Minute per repeat ) Ti တို႔ျဖစ္ပါတယ္။ တစ္ခုနဲ႔ တစ္ခုက ေျပာင္းျပန္ အခ်ဳိးက်ပါတယ္။

အခု PI Control ရဲ႕ ညီမွ်ျခင္းက

u(t) = Kp e(t) + Ki (integral) e(t’) d(t’)

ဒီေနရာမွာ

- Ki ဆိုတာ Integral Coefficient ပါ။ 

 Ki =  Kp/ Ti ျဖစ္ပါတယ္။ 

အခုဆိုယင္ Control က P နဲ႔ I ႏွစ္မ်ဳိးျဖစ္သြားေတာ့ ပို တည္ၿငိမ္ပါတယ္။ ဒါေပမဲ့ I နဲ႔ reset လုပ္ လုပ္ေပးတဲ့အတြက္ stable state ေရာက္ဖို႔ အခ်ိန္ပိုၾကာပါတယ္။ ေနာက္ၿပီး reset လိုအပ္ခ်က္အရ ေရအဝင္နႈံး ပိုျမႇင့္ေပးရတဲ့အခါ valve အက်ယ္ဆုံး (100%) ဖြင့္ေပးတာေတာင္မွ လိုအပ္တဲ့ အဝင္နႈံးက မမီေသးယင္ Integral Windup လို႔ေခၚတဲ့ ကေမာက္ကမ ျပႆနာ ၾကဳံႏိုင္ပါတယ္။ 

အဲဒါေတြကို ေျပလည္ေအာင္ (D) ကို ထည့္သုံးလာပါတယ္။ PID သုံးခုလံုးပါယင္ေတာ့ ပိုမို တည္ၿငိမ္ၿပီး response time ပိုျမန္တဲ့ Control တစ္ခု ျဖစ္လာပါတယ္။

u(t) = Kp e(t) + Ki (integral) e(t’) d(t’) + Kd de(t) / dt

ဒီေနရာမွာ 

- Kd ဆိုတာ Derivative Coefficient ပါ။

 Kd =  Kp.Td ျဖစ္ပါတယ္။ 

ညီမွ်ျခင္းေတြက ရႈပ္ေနယင္ ေက်ာ္ဖတ္လို႔ရပါတယ္။ Tuning လုပ္တဲ့အခါ အေခၚအေဝၚေတြ သိရေအာင္ ထည့္ေရးျပထားတာပါ။

(ခ) PID Control အမ်ဳိးမ်ဳိး

PID Control Algorithms လို႔ေခၚေခၚ၊ Types လို႔ ေျပာေျပာ၊ Form လို႔ ဆိုဆို Control လုပ္တဲ့ အမ်ဳိးအစား အမ်ဳိးမ်ဳိး ရွိၾကပါတယ္။ အသုံးမ်ားတဲ့ Algorithms အမ်ဳိးအစားေတြကို ေအာက္မွာ ေဖၚျပထားပါတယ္။

(၁) Interactive Algorithm

ဒီနည္းမွာ P, I, D control ေတြကို series သေဘာ တစ္ခုၿပီးမွ တစ္ခု ထိန္းခ်ဳပ္ဖို႔ စီစဥ္ထားတာမို႔ ပထမ parameter တစ္ခုရဲ႕ ေျပာင္းလဲမႈက ေနာက္ parameter ေတြကို ေျပာင္းလဲသက္ေရာက္မႈ ရွိေစပါတယ္။ ဒီနည္းကို ေခၚၾကတဲ့ နံမည္ေတြကေတာ့ “Interactive”, “Series”, “Classical”, “Real” စသျဖင့္ အမ်ဳိးမ်ဳိး ေခၚၾကပါတယ္။

(၂) Non-interactive Algorithm 

နံမည္မွာ ပါတဲ့ အဓိပၸာယ္အတိုင္း P, I, D component ေတြဟာ တစ္ခုနဲ႔တစ္ခု သက္ေရာက္မႈ မရွိေစတဲ့ နည္းကို ေခၚပါတယ္။ ဒီနည္းကို ေခၚၾကတဲ့ အမည္ကြဲေတြကေတာ့ “Non-Interactive”, “Standard”, “ISA” အစရွိသျဖင့္ ျဖစ္ပါတယ္။ တစ္ခ်ဳိ႕ စာေတြထဲမွာ ဒီနည္းကို “Parallel Algorithm” လို႔ သုံးထားတာလည္း ရွိပါတယ္။

(၃) Parallel Algorithm

ဒီနည္းကေတာ့ စာအုပ္ႀကီးနည္းလို႔ ေခၚၾကပါတယ္။ သင္ခန္းစာေတြမွာ သင္ယင္ ဒီပုံစံ ျပေလ့ရွိလို႔ပါ။ P, I, D component ေတြကို အရွင္းဆုံးပုံစံ အၿပိဳင္ဆက္ထားတာပါ။ non-interactive ရဲ႕ မူကြဲလို႔လည္း ေျပာၾကပါတယ္။ လက္ေတြ႕မွာ အသုံးနည္းပါတယ္။ ေရွ႕ပိုင္းမွာ Pneumatic နဲ႔ PID controller ေတြေဆာက္တဲ့အခါ ဒီနည္းနဲ႔ ေဆာက္လို႔ မရခဲ့ဘူး ဆိုပါတယ္။ 

ဒီတစ္ပိုင္းကို ဒီေလာက္နဲ႔ နားပါဦးမယ္။ Tuning အပိုင္း ဆက္ေရးေပးပါမယ္။

[Unicode]

(က) P, PI, PID

ဒီတစ်ခါ ဥပမာလေး တစ်ခုနဲ့ စပြောပါမယ်။ ဘွိုင်လာ (Boiler) တစ်လုံးရဲ့ ရေ level ထိန်းချုပ်တဲ့ စံနစ်လေးတစ်ခုကို မြင်ကြည့်ရအောင်။ ရေရဲ့ level ကို Set Point (SP) input အနေနဲ့ ပေးထားပြီး တည်ငြိမ်အောင် ထိန်းချုပ်မယ်ဆိုပါတော့။ ရေအထွက်နှုံးကတော့ Boiler မှာသုံးတဲ့ ရေနွေးငွေ့ အထွက်ပေါ်မူတည်နေပါတယ်။ အဲဒီအပိုင်းကို Control ရှုထောင့်ကကြည့်ယင် loading ဒါမှမဟုတ် disturbance လို့ ခေါ်ပါတယ်။ Control လုပ်ပေးမယ့် process ကတော့ ရေအဝင်နှုံး။ အသေးစိတ်ပြောရယင်တော့ water inlet valve ရဲ့ အကျဉ်းအကျယ် ဖွင့်တာပိတ်တာကို PID နဲ့ Control လုပ်မယ် ဆိုပါတော့။ Feedback (PV) ကတော့ ရေ level transmitter တစ်ခုပါ။ လိုချင်တဲ့ ရေ level (SP) ကို tank ရဲ့ 50% မှာ ထားတယ် ဆိုပါတော့။ 

အစဆုံး လက်ရှိအခြေအနေမှာ၊ Proportional (P) တစ်ခုဘဲ သုံးထားပြီး၊ ရေ အဝင်အထွက်နှုံးတွေ တူနေတဲ့အတွက်၊ တစ်ကယ်တိုင်းလို့ရတဲ့ Feedback (PV) ကလည်း 50% မှာ steady state ဖြစ်နေတယ်လို့ ယူဆပါ။

Controller Output(CO) (သို့) Manipulated Variable (MV) (သို့) u(t) ရဲ့ ညီမျှခြင်းက

u(t) = Kp e(t) 

ဒီနေရာမှာ 

- Kp ဆိုတာ proportional gain

- e(t) ဆိုတာ Error (သို့) SP - PV

တစ်ခါတလေ Kp အစား Proportional Band (PB) ကိုသုံးတာလည်း ရှိတတ်ပါတယ်။

PB = 100/Kp [%] 

အဲဒီအနေအထားကနေ loading ပိုလာတဲ့အတွက် ရေအထွက်နှုံး ပိုများလာတယ် ဆိုပါတော့။ Tank ထဲက ရေ level လျော့သွားတော့ SP-PV = Error တန်ဘိုးတစ်ခုရှိလာပါတယ်။ လက်ရှိ Kp (သို့) Proportional gain တန်ဘိုးက 2% ဆိုယင် Error နဲ့ gain မြှောက်ပြီး valve အကျဉ်းအကျယ်ပြောင်းပေးပြီး Control လုပ်ပေးတာ နောက်ဆုံး ရေ အဝင်နှုံးနဲ့ အထွက်နှုံး ညီသွားတော့ steady state ကိုရောက်သွားပါတယ်။ အဲဒီ အချိန်မှာ Tank ရဲ့ level က 45% လောက်ထိ လျော့နေပါပြီ။ SP နဲ့ ယှဉ်လိုက်တော့ 5% နည်းနေတာပေါ့။ အဲဒီလိုstable state ရောက်ပြီး offset ဖြစ်နေတတ်တာက P တစ်ခုထဲ Control လုပ်ယင် ဖြစ်တတ်တဲ့ အားနည်းချက်ပါ။ 

တစ်ကယ်လို့ gain များမယ်ဆိုယင် စောစောစီးစီး steady state ရောက်သွားတဲ့အတွက် offset တန်ဘိုး နည်းမှာပါ။ Gain တန်ဘိုး infinity လောက်ထိ တင်ပေးထားယင်တော့ offset မရှိတော့ဘူးလို့ ဆိုပါတယ်။ ဒါပေမဲ့ လက်တွေ့မှာ gain ကို infinity ထိတင်ပေးတယ်ဆိုတာ မဖြစ်နိုင်ပါဘူး။ ဒီတော့ offset ဖြစ်နေတဲ့ ရေ level ကို ပြန်ဖြည့်ပေးဘို့ လိုပါတယ်။

ပထမနည်းကတော့ Manually inlet valve ကို ပိုဖွင့်ပေးတဲ့ နည်းပါ။ အဲဒါကို reset လုပ်တယ်လို့ ခေါ်ပါတယ်။ နောက်တစ်နည်းကတော့ Integral Control (I) ကို သုံးတဲ့နည်းပါဘဲ။ အချိန်တစ်ခုရောက်တိုင်း အလိုအလျောက် reset လုပ်ပေးတဲ့ သဘောပါ။ I ရဲ့ Control parameter ဖြစ်တဲ့ Ki ဆိုတာ reset rate ပေါ့။ Controller ထုတ်လုပ်တဲ့ manufacturer ပေါ်မူတည်ပြီး I ရဲ့Control parameter နှစ်မျိုး တွေ့နိုင်ပါတယ်။ တစ်မိနစ် အတွင်း reset လုပ်တဲ့ အကြိမ်ရေ (repeat per minute) Ki နဲ့ reset လုပ်ရမယ့် ကြာချိန် (Minute per repeat ) Ti တို့ဖြစ်ပါတယ်။ တစ်ခုနဲ့ တစ်ခုက ပြောင်းပြန် အချိုးကျပါတယ်။

အခု PI Control ရဲ့ ညီမျှခြင်းက

u(t) = Kp e(t) + Ki (integral) e(t’) d(t’)

ဒီနေရာမှာ

- Ki ဆိုတာ Integral Coefficient ပါ။ 

 Ki =  Kp/ Ti ဖြစ်ပါတယ်။ 

အခုဆိုယင် Control က P နဲ့ I နှစ်မျိုးဖြစ်သွားတော့ ပို တည်ငြိမ်ပါတယ်။ ဒါပေမဲ့ I နဲ့ reset လုပ် လုပ်ပေးတဲ့အတွက် stable state ရောက်ဖို့ အချိန်ပိုကြာပါတယ်။ နောက်ပြီး reset လိုအပ်ချက်အရ ရေအဝင်နှုံး ပိုမြှင့်ပေးရတဲ့အခါ valve အကျယ်ဆုံး (100%) ဖွင့်ပေးတာတောင်မှ လိုအပ်တဲ့ အဝင်နှုံးက မမီသေးယင် Integral Windup လို့ခေါ်တဲ့ ကမောက်ကမ ပြဿနာ ကြုံနိုင်ပါတယ်။ 

အဲဒါတွေကို ပြေလည်အောင် (D) ကို ထည့်သုံးလာပါတယ်။ PID သုံးခုလုံးပါယင်တော့ ပိုမို တည်ငြိမ်ပြီး response time ပိုမြန်တဲ့ Control တစ်ခု ဖြစ်လာပါတယ်။

u(t) = Kp e(t) + Ki (integral) e(t’) d(t’) + Kd de(t) / dt

ဒီနေရာမှာ 

- Kd ဆိုတာ Derivative Coefficient ပါ။

 Kd =  Kp.Td ဖြစ်ပါတယ်။ 

ညီမျှခြင်းတွေက ရှုပ်နေယင် ကျော်ဖတ်လို့ရပါတယ်။ Tuning လုပ်တဲ့အခါ အခေါ်အဝေါ်တွေ သိရအောင် ထည့်ရေးပြထားတာပါ။

(ခ) PID Control အမျိုးမျိုး

PID Control Algorithms လို့ခေါ်ခေါ်၊ Types လို့ ပြောပြော၊ Form လို့ ဆိုဆို Control လုပ်တဲ့ အမျိုးအစား အမျိုးမျိုး ရှိကြပါတယ်။ အသုံးများတဲ့ Algorithms အမျိုးအစားတွေကို အောက်မှာ ဖေါ်ပြထားပါတယ်။

(၁) Interactive Algorithm

ဒီနည်းမှာ P, I, D control တွေကို series သဘော တစ်ခုပြီးမှ တစ်ခု ထိန်းချုပ်ဖို့ စီစဉ်ထားတာမို့ ပထမ parameter တစ်ခုရဲ့ ပြောင်းလဲမှုက နောက် parameter တွေကို ပြောင်းလဲသက်ရောက်မှု ရှိစေပါတယ်။ ဒီနည်းကို ခေါ်ကြတဲ့ နံမည်တွေကတော့ “Interactive”, “Series”, “Classical”, “Real” စသဖြင့် အမျိုးမျိုး ခေါ်ကြပါတယ်။

(၂) Non-interactive Algorithm 

နံမည်မှာ ပါတဲ့ အဓိပ္ပာယ်အတိုင်း P, I, D component တွေဟာ တစ်ခုနဲ့တစ်ခု သက်ရောက်မှု မရှိစေတဲ့ နည်းကို ခေါ်ပါတယ်။ ဒီနည်းကို ခေါ်ကြတဲ့ အမည်ကွဲတွေကတော့ “Non-Interactive”, “Standard”, “ISA” အစရှိသဖြင့် ဖြစ်ပါတယ်။ တစ်ချို့ စာတွေထဲမှာ ဒီနည်းကို “Parallel Algorithm” လို့ သုံးထားတာလည်း ရှိပါတယ်။

(၃) Parallel Algorithm

ဒီနည်းကတော့ စာအုပ်ကြီးနည်းလို့ ခေါ်ကြပါတယ်။ သင်ခန်းစာတွေမှာ သင်ယင် ဒီပုံစံ ပြလေ့ရှိလို့ပါ။ P, I, D component တွေကို အရှင်းဆုံးပုံစံ အပြိုင်ဆက်ထားတာပါ။ non-interactive ရဲ့ မူကွဲလို့လည်း ပြောကြပါတယ်။ လက်တွေ့မှာ အသုံးနည်းပါတယ်။ ရှေ့ပိုင်းမှာ Pneumatic နဲ့ PID controller တွေဆောက်တဲ့အခါ ဒီနည်းနဲ့ ဆောက်လို့ မရခဲ့ဘူး ဆိုပါတယ်။ 

ဒီတစ်ပိုင်းကို ဒီလောက်နဲ့ နားပါဦးမယ်။ Tuning အပိုင်း ဆက်ရေးပေးပါမယ်။

PID Control (1)

PID Control အေၾကာင္းေျပာယင္ Theory ေတြပါလာပါလိမ့္မယ္။ အတတ္ႏိုင္ဆုံး  လြယ္ေအာင္ ေရးၾကည့္ပါမယ္။ ျဖည္းျဖည္းဖတ္ၿပီး နားလည္ေအာင္ ႀကိဳးစားၾကည့္ၾကပါ။

အစဆုံး Close Loop Control စံနစ္ဆိုတာက စၿပီး ေျပာျပပါမယ္။ ထူးထူးျခားျခားေတာ့ မဟုတ္ပါဘူး Feedback signal တစ္ခု ျပန္ေပးတယ္ဆို Close Loop ၊ ျပန္မေပးယင္ Open Loop လို႔ မွတ္ထားလိုက္ေပါ့။ ဥပမာ တစ္ခု ေျပာပါမယ္။ ဟင္းခ်က္တဲ့ Hot Plate ေတြကို ၾကည့္လိုက္ပါ။ ဘာ Control မွ မပါဘဲ ခလုတ္တစ္ခု ဖြင့္ယင္အပူေပးတဲ့ coil မွာ မီးလာမယ္။ အပူခ်ိန္ နည္းတာမ်ားတာ ဘာမွ မဆိုင္ေတာ့ဘူး။ အဲဒါမ်ဳိးကို Open Loop ေခၚပါတယ္။ ေနာက္ မီးဖိုတစ္မ်ဳိးကေတာ့ အပူခ်ိန္ Set လုပ္လို႔ရတယ္။ ၁၆၀  ံC ကို Set ထားယင္ Thermostat က အပူခ်ိန္ကို sense လုပ္ေနပါတယ္။ တစ္နည္းအားျဖင့္ feedback ယူတာေပါ့။ ၁၆၀  ံC ေရာက္တာနဲ႔ Circuit ကို open လုပ္ေပးလိုက္လို႔  Coil မွာ မီးမလာေတာ့ဘူး။ ၁၆၀  ံC ထက္ က်သြားယင္ ျပန္ၿပီး Coil ကို လွ်ပ္စစ္စီးေစပါမယ္။ ဒါ Close loop ဥပမာတစ္ခုပါ။ 

ဒီေနရာမွာ Thermostat တစ္ခုထဲက feedback ေရာ Control ေရာ အလုပ္လုပ္သြားပါတယ္။ Control မွာလည္း အ႐ိုးစင္းဆုံး Control ဆိုေတာ့ တစ္ကယ္တမ္း တိုင္းထားၾကည့္မယ္ဆိုယင္ အပူခ်ိန္က အတက္အက် ျဖစ္ေနမွာပါ။ ၁၆၀  ံ ေက်ာ္လို႔ Coil ကို ျဖတ္လိုက္ေပမဲ့ အပူခ်ိန္ဆက္တက္ေနပါဦးမယ္။ ေနာက္ နည္းနည္းၾကာမွ ျပန္က်မွာပါ။ ၁၆၀  ံ ေအာက္ေရာက္လို႔ Coil ျပန္ On ၿပီးလည္း အပူခ်က္ခ်င္း ျပန္မတက္ဘဲ ဆက္က်ေနပါမယ္။ ၿပီးမွ ျဖည္းျဖည္းခ်င္း ျပန္တက္မွာပါ။ ထမင္းဟင္း ခ်က္တဲ့ေနရာမွာ အပူခ်ိန္ အေျပာင္းအလဲက သိပ္အေရးမႀကီးေပမဲ့ တစ္ျခား တိက်တဲ့ control လိုအပ္တဲ့ စံနစ္ေတြ၊ Process ေတြမွာ တည္ၿငိမ္ၿပီး အေျပာင္းအလဲ နည္းတဲ့ Control ေတြလိုလာပါတယ္။ အဲဒီမွာ PID Controller ေတြ သုံးလာၾကပါတယ္။

PID ဆိုတာ Proportional, Integral, Derivative ဆိုတဲ့ စာလုံး သုံးလုံးရဲ႕ အတိုေကာက္ပါ။ တစ္ခုစီက တစ္မ်ဳိးစီ အလုပ္လုပ္ပါတယ္။ P တစ္မ်ဳိးထဲသုံးတဲ့ Control, PI ႏွစ္မ်ဳိးသုံးတဲ့ Control, PID သုံးမ်ဳိးလုံး သုံးတဲ့ Control ရယ္လို႔ ရွိပါတယ္။ PD Control ကေတာ့ အရမ္းရွားပါတယ္။

အခု ေစာေစာက မီးဖိုကိုဘဲ PID Control နဲ႔ ေဆာက္ၾကည့္ၿပီး စဥ္းစားၾကည့္ရေအာင္။ ဒီတစ္ခါ Thermostat အစား PID ပါတဲ့ Temperature Controller တစ္ခုနဲ႔ feedback signal အျဖစ္ Temperature Sensor တစ္ခု တပ္ထားပါမယ္။ ဒီလိုဆိုယင္ ၁၆၀ ေက်ာ္မွ ျဖတ္မယ္။ ၁၆၀ ေအာက္မွာ On မယ္ဆိုတဲ့ ႐ိုးစင္းတဲ့ Control မဟုတ္ေတာ့ပါဘူး။ ၁၆၀ နဲ႔ ေဝးေနေသးယင္ ေတာက္ေလွ်ာက္ On ထားမယ္။ ၁၆၀ နဲ႔ နီးလာတာနဲ႔ အမွ် On/Off duty cycle ေတြ တစ္ျဖည္းျဖည္း ေျပာင္း ေပးၿပီး ၁၆၀ ဝန္းက်င္မွာ တည္ၿငိမ္တဲ့ အပူခ်ိန္ကို ထိမ္းထားေပးမွာပါ။

Control System တစ္ခုမွာ လိုခ်င္တဲ့ တန္ဘိုး Set Point (SP) ရွိပါမယ္။ ေနာက္ တစ္ကယ္တိုင္းလို႔ရတဲ့ တန္ဘိုး feedback signal တစ္နည္းအားျဖင့္ Process Variable (PV) ရွိပါမယ္။ အဲဒီ SP နဲ႔ PV ရဲ႕ ကြာဟခ်က္က Error ေပါ့။ တနည္းေျပာရယင္ SP ထဲကေန PV ကို ျပန္နႈတ္ၿပီး Control လုပ္တာမို႔ Negative feedback လို႔ ေခၚပါတယ္။ (ပုံမွာၾကည့္ပါ။) Negative Feedback ရဲ႕သဘာဝအရ Error ကတစ္ျဖည္းျဖည္း နည္းလာၿပီး တည္ၿင္ိမ္မႈ ( stable state) ကို ရေစပါတယ္။ Positive Feedback ဆိုယင္ေတာ့ SP နဲ႔ PV ေပါင္းၿပီး Control လုပ္တဲ့အတြက္ output က တစ္ျဖည္းျဖည္း မ်ားသြားမွာ ျဖစ္ပါတယ္။ 

အခု Negative Feedback သုံးထားတာဆိုေတာ့ Error တန္ဘိုးေပၚမူတည္ၿပီး Coil ကို ဖြင့္ျခင္းပိတ္ျခင္း နဲ႔ ထိန္းခ်ဳပ္သြားတာမို႔ Error ကတစ္ျဖည္းျဖည္း နည္းသြားၿပီး တည္ၿငိမ္တဲ့ ရလာဒ္ ရေစပါတယ္။ 

 

အခု Control လုပ္ေပးတဲ့ အလယ္ပိုင္းကို P ရယ္၊ I ရယ္၊ D ရယ္ Control သုံးခုခြဲၿပီး ျပန္ေပါင္းထားတယ္လို႔ ျမင္ၾကည့္လိုက္ပါ။ (ပုံၾကည့္ပါ။) အဲဒီမွာ PID  တစ္ခုစီရဲ႕ သက္ေရာက္ပုံေျပာပါမယ္။ ျမင္သာေအာင္ ပစၥဳပၸန္၊ အတိတ္၊ အနာဂါတ္ လို႔မွတ္ထားလိုက္ပါ။ 

~ Proportional က ပစၥဳပၸန္ လက္ရွိ feedback တန္ဘိုးရဲ႕ Error ေပၚမူတည္လို႔ gain နဲ႔ ေျမႇာက္ၿပီး Control လုပ္ပါတယ္။ 

~ Integral ကေတာ့ အတိတ္က အခ်ိန္တစ္ခုအတြင္းျဖစ္ခဲ့တဲ့ ေျပာင္းလဲမႈနႈံးကို တြက္ၿပီး Control လုပ္ပါတယ္။ 

~ Derivative ကေတာ့ အနာဂါတ္ အခ်ိန္တစ္ခုမွာ တည္ၿငိမ္မႈရႏိုင္ေစမယ့္ အေျခအေနကို ခန္႔မွန္း တြက္ထုတ္ၿပီး Control လုပ္ပါတယ္။

ဘာလို႔ သုံးမ်ဳိးသုံထားတာလဲ။ P တစ္မ်ဳိးထဲဆိုယင္ Error တန္ဘိုး တစ္ခုမွာ တစ္ျဖည္းျဖည္း stable ျဖစ္သြားေပမဲ့ offset တန္ဘိုးတစ္ခု ရွိေနဦးမွာပါ။ I ေပါင္းထည့္လိုက္တဲ့အခါ offset ေပ်ာက္သြားၿပီး ပို stable ျဖစ္ေပမဲ့ အခ်ိန္တစ္ခုထိ ေစာင့္ရပါတယ္။ ေနာက္ၿပီး I တန္ဘိုး Range Limit တစ္ခုေက်ာ္သြားယင္ output တန္ဘိုးက ျပန္မက်ေတာ့ဘဲ ဆက္တိုက္တက္ၿပီး ကေမာက္ကမျဖစ္တာမ်ဳိး ရွိပါတယ္။ ေနာက္ဆုံုး D ပါထပ္ထည့္လိုက္ေတာ့ အဲဒီျပႆနာကို ေက်ာ္လႊားႏိုင္သလို Response time လည္း ပိုျမန္လာပါတယ္။

အေျခခံျဖစ္တဲ့ ဒီတစ္ပိုင္းကို ေသခ်ာဖတ္ထားပါဦး။ မတူတဲ့ Control Algorithm ေတြနဲ႔ Tuning အပိုင္း ေနာက္ထပ္ ေရးေပးပါဦးမယ္။

 

[Unicode]

PID Control အကြောင်းပြောယင် Theory တွေပါလာပါလိမ့်မယ်။ အတတ်နိုင်ဆုံး  လွယ်အောင် ရေးကြည့်ပါမယ်။ ဖြည်းဖြည်းဖတ်ပြီး နားလည်အောင် ကြိုးစားကြည့်ကြပါ။

အစဆုံး Close Loop Control စံနစ်ဆိုတာက စပြီး ပြောပြပါမယ်။ ထူးထူးခြားခြားတော့ မဟုတ်ပါဘူး Feedback signal တစ်ခု ပြန်ပေးတယ်ဆို Close Loop ၊ ပြန်မပေးယင် Open Loop လို့ မှတ်ထားလိုက်ပေါ့။ ဥပမာ တစ်ခု ပြောပါမယ်။ ဟင်းချက်တဲ့ Hot Plate တွေကို ကြည့်လိုက်ပါ။ ဘာ Control မှ မပါဘဲ ခလုတ်တစ်ခု ဖွင့်ယင်အပူပေးတဲ့ coil မှာ မီးလာမယ်။ အပူချိန် နည်းတာများတာ ဘာမှ မဆိုင်တော့ဘူး။ အဲဒါမျိုးကို Open Loop ခေါ်ပါတယ်။ နောက် မီးဖိုတစ်မျိုးကတော့ အပူချိန် Set လုပ်လို့ရတယ်။ ၁၆၀  ံC ကို Set ထားယင် Thermostat က အပူချိန်ကို sense လုပ်နေပါတယ်။ တစ်နည်းအားဖြင့် feedback ယူတာပေါ့။ ၁၆၀  ံC ရောက်တာနဲ့ Circuit ကို open လုပ်ပေးလိုက်လို့  Coil မှာ မီးမလာတော့ဘူး။ ၁၆၀  ံC ထက် ကျသွားယင် ပြန်ပြီး Coil ကို လျှပ်စစ်စီးစေပါမယ်။ ဒါ Close loop ဥပမာတစ်ခုပါ။
ဒီနေရာမှာ Thermostat တစ်ခုထဲက feedback ရော Control ရော အလုပ်လုပ်သွားပါတယ်။ Control မှာလည်း အရိုးစင်းဆုံး Control ဆိုတော့ တစ်ကယ်တမ်း တိုင်းထားကြည့်မယ်ဆိုယင် အပူချိန်က အတက်အကျ ဖြစ်နေမှာပါ။ ၁၆၀  ံ ကျော်လို့ Coil ကို ဖြတ်လိုက်ပေမဲ့ အပူချိန်ဆက်တက်နေပါဦးမယ်။ နောက် နည်းနည်းကြာမှ ပြန်ကျမှာပါ။ ၁၆၀  ံ အောက်ရောက်လို့ Coil ပြန် On ပြီးလည်း အပူချက်ချင်း ပြန်မတက်ဘဲ ဆက်ကျနေပါမယ်။ ပြီးမှ ဖြည်းဖြည်းချင်း ပြန်တက်မှာပါ။ ထမင်းဟင်း ချက်တဲ့နေရာမှာ အပူချိန် အပြောင်းအလဲက သိပ်အရေးမကြီးပေမဲ့ တစ်ခြား တိကျတဲ့ control လိုအပ်တဲ့ စံနစ်တွေ၊ Process တွေမှာ တည်ငြိမ်ပြီး အပြောင်းအလဲ နည်းတဲ့ Control တွေလိုလာပါတယ်။ အဲဒီမှာ PID Controller တွေ သုံးလာကြပါတယ်။

PID ဆိုတာ Proportional, Integral, Derivative ဆိုတဲ့ စာလုံး သုံးလုံးရဲ့ အတိုကောက်ပါ။ တစ်ခုစီက တစ်မျိုးစီ အလုပ်လုပ်ပါတယ်။ P တစ်မျိုးထဲသုံးတဲ့ Control, PI နှစ်မျိုးသုံးတဲ့ Control, PID သုံးမျိုးလုံး သုံးတဲ့ Control ရယ်လို့ ရှိပါတယ်။ PD Control ကတော့ အရမ်းရှားပါတယ်။
အခု စောစောက မီးဖိုကိုဘဲ PID Control နဲ့ ဆောက်ကြည့်ပြီး စဉ်းစားကြည့်ရအောင်။ ဒီတစ်ခါ Thermostat အစား PID ပါတဲ့ Temperature Controller တစ်ခုနဲ့ feedback signal အဖြစ် Temperature Sensor တစ်ခု တပ်ထားပါမယ်။ ဒီလိုဆိုယင် ၁၆၀ ကျော်မှ ဖြတ်မယ်။ ၁၆၀ အောက်မှာ On မယ်ဆိုတဲ့ ရိုးစင်းတဲ့ Control မဟုတ်တော့ပါဘူး။ ၁၆၀ နဲ့ ဝေးနေသေးယင် တောက်လျှောက် On ထားမယ်။ ၁၆၀ နဲ့ နီးလာတာနဲ့ အမျှ On/Off duty cycle တွေ တစ်ဖြည်းဖြည်း ပြောင်း ပေးပြီး ၁၆၀ ဝန်းကျင်မှာ တည်ငြိမ်တဲ့ အပူချိန်ကို ထိမ်းထားပေးမှာပါ။

Control System တစ်ခုမှာ လိုချင်တဲ့ တန်ဘိုး Set Point (SP) ရှိပါမယ်။ နောက် တစ်ကယ်တိုင်းလို့ရတဲ့ တန်ဘိုး feedback signal တစ်နည်းအားဖြင့် Process Variable (PV) ရှိပါမယ်။ အဲဒီ SP နဲ့ PV ရဲ့ ကွာဟချက်က Error ပေါ့။ တနည်းပြောရယင် SP ထဲကနေ PV ကို ပြန်နှုတ်ပြီး Control လုပ်တာမို့ Negative feedback လို့ ခေါ်ပါတယ်။ (ပုံမှာကြည့်ပါ။) Negative Feedback ရဲ့သဘာဝအရ Error ကတစ်ဖြည်းဖြည်း နည်းလာပြီး တည်ြငိမ်မှု ( stable state) ကို ရစေပါတယ်။ Positive Feedback ဆိုယင်တော့ SP နဲ့ PV ပေါင်းပြီး Control လုပ်တဲ့အတွက် output က တစ်ဖြည်းဖြည်း များသွားမှာ ဖြစ်ပါတယ်။
အခု Negative Feedback သုံးထားတာဆိုတော့ Error တန်ဘိုးပေါ်မူတည်ပြီး Coil ကို ဖွင့်ခြင်းပိတ်ခြင်း နဲ့ ထိန်းချုပ်သွားတာမို့ Error ကတစ်ဖြည်းဖြည်း နည်းသွားပြီး တည်ငြိမ်တဲ့ ရလာဒ် ရစေပါတယ်။

အခု Control လုပ်ပေးတဲ့ အလယ်ပိုင်းကို P ရယ်၊ I ရယ်၊ D ရယ် Control သုံးခုခွဲပြီး ပြန်ပေါင်းထားတယ်လို့ မြင်ကြည့်လိုက်ပါ။ (ပုံကြည့်ပါ။) အဲဒီမှာ PID  တစ်ခုစီရဲ့ သက်ရောက်ပုံပြောပါမယ်။ မြင်သာအောင် ပစ္စုပ္ပန်၊ အတိတ်၊ အနာဂါတ် လို့မှတ်ထားလိုက်ပါ။
~ Proportional က ပစ္စုပ္ပန် လက်ရှိ feedback တန်ဘိုးရဲ့ Error ပေါ်မူတည်လို့ gain နဲ့ မြှောက်ပြီး Control လုပ်ပါတယ်။
~ Integral ကတော့ အတိတ်က အချိန်တစ်ခုအတွင်းဖြစ်ခဲ့တဲ့ ပြောင်းလဲမှုနှုံးကို တွက်ပြီး Control လုပ်ပါတယ်။
~ Derivative ကတော့ အနာဂါတ် အချိန်တစ်ခုမှာ တည်ငြိမ်မှုရနိုင်စေမယ့် အခြေအနေကို ခန့်မှန်း တွက်ထုတ်ပြီး Control လုပ်ပါတယ်။

ဘာလို့ သုံးမျိုးသုံထားတာလဲ။ P တစ်မျိုးထဲဆိုယင် Error တန်ဘိုး တစ်ခုမှာ တစ်ဖြည်းဖြည်း stable ဖြစ်သွားပေမဲ့ offset တန်ဘိုးတစ်ခု ရှိနေဦးမှာပါ။ I ပေါင်းထည့်လိုက်တဲ့အခါ offset ပျောက်သွားပြီး ပို stable ဖြစ်ပေမဲ့ အချိန်တစ်ခုထိ စောင့်ရပါတယ်။ နောက်ပြီး I တန်ဘိုး Range Limit တစ်ခုကျော်သွားယင် output တန်ဘိုးက ပြန်မကျတော့ဘဲ ဆက်တိုက်တက်ပြီး ကမောက်ကမဖြစ်တာမျိုး ရှိပါတယ်။ နောက်ဆုံး D ပါထပ်ထည့်လိုက်တော့ အဲဒီပြဿနာကို ကျော်လွှားနိုင်သလို Response time လည်း ပိုမြန်လာပါတယ်။

အခြေခံဖြစ်တဲ့ ဒီတစ်ပိုင်းကို သေချာဖတ်ထားပါဦး။ မတူတဲ့ Control Algorithm တွေနဲ့ Tuning အပိုင်း နောက်ထပ် ရေးပေးပါဦးမယ်။